Tissot  representó  un  punto  sobre  el  elipsoide mediante  un  círculo  finito  con radio ‘unidad’.

Considerando ‘a’ y ‘b’ como los radios resultantes al transformar esta circunferencia, representada sobre el elipsoide, en una elipse representada sobre el plano, tenemos que en casi cualquier sistema de transformación las magnitudes ‘a’ y ‘b’ se convertirán en mayores o menores que la unidad.

Mediante el análisis de los cambios geométricos del paso del círculo a una elipse, se determina el valor de la distorsión angular y el aumento o disminución en la representación de la superficie que se ha producido en cualquier punto de la proyección. 

Por tanto, la elipse indicatriz de Tissot se usa para ilustrar gráficamente las distorsiones lineales, angulares y de área de los mapas.

Proyección cilíndrica equidistante de Lambert

El teorema de Tissot, dice que cualquiera que sea el sistema de transformación en  cada  punto  de  la  superficie  esférica, existen  por  lo menos  un par de direcciones ortogonales que serán también ortogonales sobre la proyección. Las direcciones emparejadas mantenidas como ortogonales en la proyección se llaman ‘Direcciones Principales’, y será aquí donde se produzcan las desviaciones máximas de el factor de escala.

A continuación, se muestran algunas de las proyecciones más utilizadas y su distorsión en función de la elipse de Tissot.

- Proyección cilíndrica equivalente de Lambert

- Proyección de Mercator

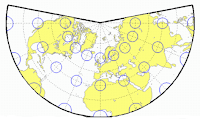
- Proyección cónica conforme de Lambert