UTM responde a las siglas de Universal Transversa de Mercator, aunque también es llamada proyección Gauss-Krüger, debido a los cartógrafos que la idearon.
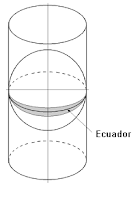
Esta proyección está basada en una proyección desarrollable, desarrollada haciendo uso de un cilindro tangente al elipsoide. Se denomina transversa debido a que la tangencia no es realizada sobre un paralelo, como se solía hacer (Proyección Mercator), si no sobre uno de los meridianos, siendo ese meridiano la única línea automecoica de dicha proyección.


Su "universalidad" se logra empleando distintos cilindros correspondientes a varios meridianos, separados entre sí 6º, de manera que cada huso de 6º emplea uno distinto.
Como ya dijimos, en cada proyección sólo el meridiano origen de cada uso y el Ecuador aparecen como rectas (perpendiculares entre ellas), no siéndolo los demás paralelos y meridianos. Tampoco son arcos de circunferencia.

Este sistema queda limitado a representar latitudes inferiores a 80º, por lo que los polos no se suelen representar.

En España hay que utilizar 3 husos distintos para representar la Península y Baleares y otros dos para Canarias.

Sistema de coordenadas

Al desarrollar esta proyección, se obtiene un sistema de coordenadas formado por la proyección del Ecuador, que forma el eje X y la proyección del meridiano tomado como tangencia, que constituirá el eje Y, formando un sistema de coordenadas cartesianas.
El número del huso se tomará a partir del del antemeridiano de Greenwich, en sentido Oeste-Este, de manera que en España obtenemos los husos 27, 28, 29, 30 y 31.
Para las ordenadas se toma como eje una recta paralela al meridiano central, 500 km al Oeste, evitando las coordenadas negativas, mientras que para las abscisas se utiliza el propio Ecuador.

La proyección Mercator constituyó un verdadero avance en la Cartografía al ser utilizada en 1569 por su inventor. Gerhard Kremer (Mercator). Mercator encontró la contrucción geométrica, que tranformando los meridianos y paralelos en una red rectangular, conservase los ángulos. Se trata de la primera proyección CONFORME hallada.

Estamos hablando de una proyección cilíndrica, de manera que este cilindro queda circunscrito al Ecuador terrestre, sobre el que se van espaciando los paraleloes al aumentar las latitudes, de forma que la razón de distancias entre paralelos y meridianos es la misma que en la esfera.

Sobre esta red de meridianos y paralelos pueden trazarse rectas oblicuas que cortarán a los meridianos bajo un ángulo constante, y que representan curvas que en la Tierra también forman ángulo constante con los meridianos.
Estas curvas reciben el nombre de loxodrómicas, y permitien a un barco mantener un rumbo constante, lo que hace que sea fácil de conservar.
Por esto los barcos navegaban siguiendo las loxodrómicas, aunque este camino era mayor que si navegaban a través de la ortodrómica (que une puntos mediante el arco de círculo máximo).

Fue en realidad, en la busqueda de representar estas loxodrómicas como Mercator ideó esta proyección.

Hemos visto que aquí se conservan los ángulos, pero sin embargo, las distancias sufren deformaciones grandes, mayores a medida que la latitud crece, de manera que los polos nunca son representados. Esto es así debido a que la escala varía en función de la latitud.


Debido a esto, suele acompañarse estas cartas con una escala gráfica donde se indica la distancia en las diferentes latitudes, y se indica cual es el meridiano origen.

La proyección cónica de Lambert es de una de las proyecciones cónicas más empleadas. Fue presentada en 1772 por Lambert bajo su nombre, con una aplicación principal para regiones de pequeña extensión.

Su construcción comienza por la representación de la esfera sobre una superficie auxiliar, que se trata de un cono circunscrito a lo largo de un paralelo. Posteriormente este paralelo se desarrolla sobre un plano. No se trata de una proyección geométrica, debido a que la separación entre los paralelos se calcula analíticamente de forma que, se obtiene una representación conforme, tal y como ocurre en la proyección de Mercator.

Los meridianos aparecen como rectas concurrentes (en el punto que corresponde al vértice del cono en el desarrollo) y forman ángulos iguales entre sí los que tienen la misma diferencia de longitud.
Los paralelos por su parte, se representan mediante circunferencias concéntricas (respecto al punto anteriormente mencionado).


Se trata de una proyección que fue reglamentaria en todos los mapas militares a gran escala, eligiéndose el cono tangente a lo largo del paralelo de 40º.
Para el cálculo definitivo, se decidió que dicho cono secante a dos paralelos situados, aproximadamente, a 2º 50' al Norte y al Sur del paralelo 40º.

Coordenadas Lambert.

En España, la cartografía militar ha empleado durante mucho tiempo las coordenadas y la cuadrícula de este sistema. Como ejes OY, OX, se eligieron como meridiano central el de Madrid y la recta perpendicular en su intersección con el paralelo 40º, siendo el origen un punto próximo a Aranjuez.

Por tanto, las rectas de la cuadrícula no son ni meridianos ni paralelos, si no, paralelos a ellos.
Además, para evitar las coordenadas negativas se trasladó el origen 600 kilómetros al Oeste y 600 kilómetros al Sur.


Sin embargo, para los mapas de Canarias, se emplea otro cono auxiliar distinto, donde cuyo centro del mapa, con coordenadas x = 400, y = 400, es la intersección del meridiano de longitud 12º al Oeste de Madrid y el paralelo de latitud 28º 30'.

A la hora de tratar el tema de la proyecciones, todo aquel que esté un poquito familiarizado con ellas, le vendrán a la cabeza aquellas famosas, como puede ser Mercator o Lambert, al ser una de las más utilizadas.

Casi toda proyección debe guardar una de las proporciones equivalentes a la realidad (Distancias, ángulos o áreas), sin embargo, existe otro grupo donde la distorsión se produce en todas ellas, pero resulta lo menor posible.En este último caso encuadraríamos a la proyección Winkel-Tripel, propuesta por Oswald Winkel en 1921.


Cabe destacar que esta proyección deriva de una media aritmética entre la proyección de Aitoff y una proyección cilíndrica equidistante.

Se caracteriza además por se una proyección donde se pueden plasmar los polos, llegando a representar latidudes de más de 90 grados, resultado muy interesante para la representación total. Actualmente es considerada una de las mejores proyecciones para representar toda la superficie terreste, destacandado que desde 1998 es la proyección estandar para los mapamundis realidados por National Geographic Society.



Además, actualmente he observado que esta proyección se ha utilizado para poder plasmar la localización de terremotos registrados sobre toda la Tierra, debido sobre todo a la representación de esas latitudes de los polos.

Uno de los principales problemas que plantea la Cartografía, es la búsqueda de solución a la representación de la superficie "esférica" de la Tierra sobre una superficie plana, minimizando las deformaciones.

Como esto es imposible, se buscan soluciones aproximadas de manera que nuestro mapa resulte lo más fiel posible a lo que en realidad existe. Es por esto, por lo que utilizamos las proyecciones cartográficas.

Una proyección cartográfica será la solución establecida para resolver el problema de proyectar una superficie tridimensional sobre una superficie plana (papel), consiguiendo que las deformaciones sean mínimas y controladas. Por tanto, una proyección cartográfica será la conversión de coordenadas desde un sistema de coordenadas geodésico a un sistema de coordenadas plano.


Una manera de clasificar las proyecciones cartográficas, será en función de las propiedades métricas de éstas, donde llegamos a distinguir 4 grupos: